生物統計

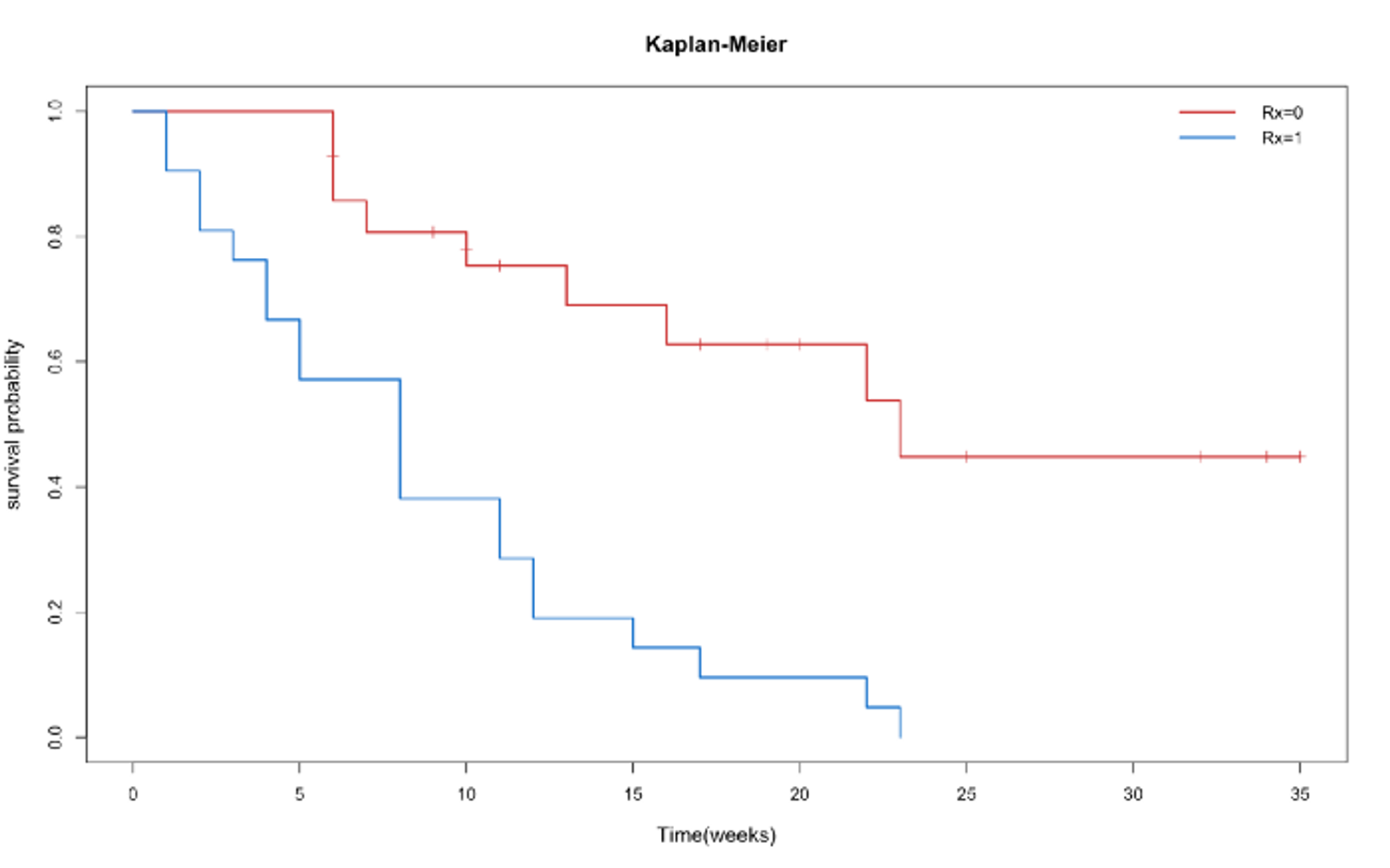
本文探討某疾病的死亡率以及存活率進行存活分析。 設定一個起始時間(starting point)，例如確診某疾病的時間或是接受手術的時間點，並且觀察特定事件(event)(i.e., 死亡或疾病復發)，進一步計算疾病的存活率。存活分析的資料特色為依變項(Y)同時為連續且具有類別的性質且有設限資料 (censoring)。 程式範例 讀檔: read.csv Anderson <- read.csv(“路徑/Anderson.csv”) 使用套件: survival 存活分析需使用套件 “ survival ” ，若未安裝以指令 “library(packagename)” 呼叫套件，再執行 “install.packages(“packagename”)”。 install.packages(“survival”)library(survival) 轉換資料格式: Surv 在存活分析中，反應變數由存活時間(Survival time)及事件(Event)的狀態兩種變數所組成，需要將資料格式轉換為存活資料的格式，藉由 “Surv()” 指令 my.surv <- Surv(Anderson$Survt, Anderson$Relapse==1) 其中 Anderson$Survt 為存活時間，Anderson$Relapse為事件狀態(0=設限; 1=復發，即發生事件)。 存活資料: survfit 接著，利用指令“survfit( )”獲得 K-M 估計式，其中 “survfit( )” 的 “my.surv” 指存活資料，因為希望看到不同治療組別的存活曲線是否有明顯差異，因此“~ Rx”指將存活資料以不同的治療組別進行計算，檔案為“Anderson”。 km.fit <- survfit(my.surv~ Rx, data=Anderson ) 繪製: plot 再利用指令 “plot()” 完成繪製圖形。 plot(km.fit, conf.int=F, mark.time=T, col=c(“brown3”, “dodgerblue3”),lwd=2, cex.lab=1.2, cex.main=1.3, main=”Kaplan-Meier”, xlab=”Time(weeks)”, ylab=”survival probability”) 其中 “conf.int = T/F” 表示是否要加入信賴區間，“mark.time = T/F” 為是否要將設限時間標示出來，“col=” 線的顏色，“ lwd＝” 線的粗細， “cex.lab=” 座標軸字體大小，“cex.main=”主標題字體大小，“main=” 標題名稱， “xlab=” x軸名稱，“ ylab=” y 軸名稱。 圖例: legend 最後一個步驟使用指令“legend()”告知 R，該如何製作這張圖的圖例。 legend(“topright”, col=c(“brown3”, “dodgerblue3”),lwd=2, bty=”n”, legend=c(names(km.fit$strata[1]), names(km.fit$strata[2]) “topright” 為圖例位置，“col=”顏色與圖中的線一樣，“bty=n”表示不要有外框， “names(km.fit$strata[1])” 表示以 “km.fit”分層中的第一個分層的名稱命名。即完成 Kaplan-Meier 的繪製。